Writing a keygen for a 20+ year old game

Introduction
The early 2000s were a simpler time: chunky monitors, physical game CDs, and of course, serial keys printed on those jewel cases that always seemed to go missing. Now, years later, you’ve got an old favorite game in your hands but no way to get past the long-forgotten DRM. That’s where reverse engineering and keygens come in handy.
In this post, we’ll walk through how we can reverse engineered the serial verification of a 20+ year-old game. It’s a mix of nostalgia and technical exploration, digging into how these protections were built and, of course, how we can bypass them today. Just a reminder-this is for educational purposes only, meant to give insight into the workings of DRM from an era gone by.
Locate the serial key verification function
Let’s dive straight into the technical process. The goal here is to identify the function that verifies the game’s serial key. Our goal here was to track the serial key’s handling in memory during the installation process. To do this, I launched the INSTALL.exe from the mounted ISO using x32dbg for live debugging. When launching the install CD, we can reach the following window expecting our serial key to proceed.
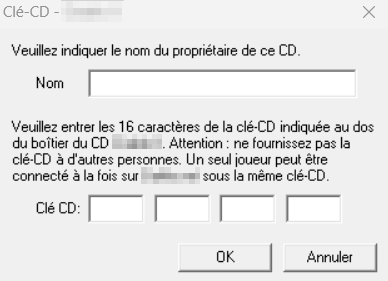
Once the serial key window appeared, I navigated to the Handles section, refreshed the list, and located the “OK” button. I then set a breakpoint on the WM_LBUTTONUP event, which triggers when the “OK” button is clicked. This allowed me to intercept the moment the user confirms their serial key input.
From here, I followed the code execution as the installer processed the serial key. Chunk by chunk, the key was copied into memory until I reached the critical function at 0x0041B1EB. Here, I could see the serial key being checked against the expected values, suggesting that this function plays a central role in the verification process.
With this information, I opened the function at 0x0041B1EB in Ghidra for deeper analysis of the serial verification logic.
Reverse the serial checking algorithm
Now that we’ve located the key verification function, it’s time to understand how it works. We’ll look at the instructions responsible for comparing the input with the expected values. The key takeaway is figuring out the logic behind how the installer decides whether a serial key is legitimate or not.
Trivial Bypass
As we can expect, the 0x0041B1EB needs to return 1 for success. A quick-and-dirty way to bypass the serial check entirely is to force the function to always return such value. This simple assembly tweak is a classic example of patching, but it’s not the fun that we’re looking for.
_0041B1EB: mov rax, 1
ret
Serial Check Logic
Now, we’re going to take a deeper dive into the inner workings of the serial key validation algorithm. We’ll break down the steps involved in processing the key: from character transformations to bitmask calculations, and how each part of the serial key gets validated. This will lay the foundation for what we need to know to write a valid key generator later on.
Serial Key Charset:
Based on the input window and the actual code, we can see that each serial key needs to be 16 characters long. These characters are compared to a hardcoded lookup table filled with 0xff values, except for 24 positions with values ranging from 0x0 to 0x17. If the lookup table, indexed by the ASCII character value, returns something lower than 0x18, the character is considered valid.
lookup_table = b'\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\x00\xff\x01\xff\x02\x03\x04\x05\xff\xff\xff\xff\xff\xff\xff\xff\x06\x07\x08\x09\x0a\x0b\x0c\xff\x0d\x0e\xff\x0f\x10\xff\x11\xff\x21\xff\x13\xff\x14\x15\x16\xff\x17\xff\xff\xff\xff\xff\xff\xff\x06\x07\x08\x09\x0a\x0b\x0c\xff\x0d\x0e\xff\x0f\x10\xff\x11\xff\x12\xff\x13\xff\x14\x15\x16\xff\x17\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff\xff'
By checking all valid positions, we can see that the character set for our serial key needs to come from the following (both lower and upper case letters are valid):
2, 4, 6, 7, 8, 9, B, C, D, E, F, G, H, J, K, M, N, P, R, T, V, W, X, Z
Transform and Bitmask:
After the charset verification, the serial key is transformed and a bitmask is created. This bitmask helps track any overflows that occur during the transformation process and is essential for validating the key.
To begin with, we examine the serial key two characters at a time. For each pair, we look up their corresponding values from the lookup_table. We then calculate a combined value by multiplying the value of the first character by 0x18 and adding the value of the second character.
If the computed value exceeds 0xff, this indicates an overflow. To handle this, we subtract 0x100 from the computed value and set a bit in the bitmask to mark that an overflow occurred. Each bit in the 8-bit bitmask corresponds to a position in the serial key.
After adjusting for overflow, we convert the adjusted value back into hexadecimal characters. The transformed characters are then updated in the serial key. Additionally, we shift the bitmask left by one position to prepare for processing the next pair of characters.
def transform_key(serial):
for i in range(0, 0x10,2):
first = lookup_table[ord(serial[i])]
second = lookup_table[ord(serial[i+1])]
val = first * 0x18 + second
if (0xff < val):
val -= 0x100
bitmask |= bit
serial[i] = hexChar(val >> 4) # hexChar: e.g., 0xf -> "F"
serial[i+1] = hexChar(val % 0x10)
bit = bit << 1
return serial, bitmask
Checksum:
Following the bitmask, a checksum is computed on the new serial key.
def checksum(serial):
checksum = 3
for current_char in serial:
shifted_mask = checksum << 1
checksum += shifted_mask ^ hexCharValue(current_char) # e.g., "F" -> 0xf
return checksum &= 0xff
This basic checksum can be seen as the following sequence:
\[X_0 = 3\] \[X_i = 2X_{i-1} \oplus a_i + X_{i-1}\]With \(a_i\) the value represented by the current char of the serial key. However, only the last byte of the resul will be compared to the previous bitmask, making it a simple 256 bits checksum. If the check is valid, we enter a shuffle operation.
Shuffle:
At this point, the serial key will undergo a permutation. This shuffle operation might initially appear to swap the all key, but it actually performs a really straightforward transformation. The purpose of this operation is to rearrange the serial key, moving the middle bytes to the front and end of the key.
def shuffle(serial):
for i in range(16, 0, -1):
computed_index = (i * 0x11 + 7) % 0x10;
tmp = serial[i];
serial[i] = serial[computed_index];
serial[computed_index] = tmp;
return serial
To illustrate, consider the following example with a dummy serial key:
Original: 2244 6677 8899 BBCC
Shuffled: 6722 4468 99BB CC78
In this shuffled version, you’ll notice that the middle bytes have been moved to the front and end of the key.
Magic Mask:
The magic mask operation is a crucial step in transforming the serial key by applying a self-modifying mask to certain characters. This operation uses a hardcoded magic number and processes each character of the serial key based on its value.
def magic_mask(serial):
magic_number = 0x13ac9741
for i in range(0xf, -1, -1):
if (serial[i] < '8'):
serial[i] = chr(ord(serial[i]) ^ magic_number & 7)
magic_number = magic_number >> 3
elif (serial[i] < 'A'):
serial[i] = chr(ord(serial[i]) ^ i & 1)
return serial
The function starts with a predefined magic number, 0x13ac9741, which is used to transform the characters in the serial key. Here’s a step-by-step breakdown of the process:
- Iteration: The function iterates from the end of the serial key (i = 15) to the beginning (i = 0), processing each character.
- Character Transformation:
- If the character is less than ‘8’, it undergoes a transformation using the magic number. Specifically, the character is XOR-ed with the least significant 3 bits of the magic number, and then the magic number is right-shifted by 3 bits for the next iteration.
- If the character is less than ‘A’, it is transformed by XOR-ing it with the least significant bit of the index.
This approach modifies the characters based on their value and position in the key, applying a dynamic transformation using the magic number. The result is a serial key where certain characters have been altered based on the magic mask logic.
Serial Check:
The actual serial key validation combines all the processes we’ve explored: transformations, checksums, shuffles, and masks. By understanding this check in detail, we can effectively replicate it to ensure that our keygen generates valid keys. The only remaining check is to see if new serial key start with “06” or “07”.
Here’s the check_serial function that encapsulates the entire verification process:
def check_serial(serial):
new_serial, computed_bitmask = transform_key(serial)
check = checksum(new_serial)
if (check == computed_bitmask):
shuffled_serial = shuffle(new_serial)
masked_serial = magic_mask(shuffled_serial)
return masked_serial[0] == '0' and masked_serial[1] == '6' or masked_serial[1] == '7')
return False
Additional note: For the game’s expansion, the same key verification mechanism is used but with a slight variation, the characters ‘6’ and ‘7’ are replaced with ‘N’ and ‘C’.
Writing the keygen
Finally, with all the algorithm pieces in hand, we walk through writing the actual keygen.
As a recap, here are all the properties our serial needs to match:
- It must be 16 characters long, using only the defined charset.
- The checksum of its transformation must match the overflow bitmask.
- After shuffling and applying the magic number mask, it must start with “06” or “07”.
def gen_serial():
charset = [
'2', '4', '6', '7', '8', '9', 'B', 'C',
'D', 'E', 'F', 'G', 'H', 'J', 'K', 'M',
'N', 'P', 'R', 'T', 'V', 'W', 'X', 'Z']
serial = ""
for i in range(16):
serial += charset[random.randrange(len(charset))]
return serial
if __name__ == '__main__':
while True:
serial = gen_serial()
if check_serial(serial):
print("Success!\nCD key:\t" + serial)
With this, our keygen can now successfully generate valid serial keys!
Conclusion
In this exploration, we’ve tackled the challenge of an old game’s DRM system using a practical approach. By analyzing the serial key verification algorithm, we’ve gained insight into its inner workings and used this understanding to develop a keygen that mimics the original check.
Our keygen works by simulating the validation process and employing a brute-force strategy to randomly generate and test serial keys until it finds one that succeeds. This method highlights the importance of comprehending the verification logic and demonstrates a straightforward way to bypass the game’s protection.
Thank you for joining me on this exploration.
Disclaimer
This article is intended for educational purposes only. The author is not responsible for any damages, unauthorized access, or illegal activities that may arise from this content. This demonstration is a product of research driven by a passion for cybersecurity.